Group Theory

Chapters

1. Integers:Unique division with remainder of whole numbers, various lemmas on prime factorization, Euclidian Algorithm and Generalized Euclidian Algorithm.
2. Groups:Definition of monoid and group, examples. Left-axioms, right-axioms, their equivalence.
3. Subgroups, Homomorphisms, Direct Products: with Chinese remainder theorem for integers.
4. Permutation Groups: cycle factorization, sign, Cayley’s theorem. Alternating groups
5. Generators, Order, Index: cosets, Lagrange’s theorem, totient function & Euler’s theorem of prime congruences, Fermat’s small theorem as consequence.
6. Normal Subgroups, Factor Groups: e.g. Commutator subgroup and abelian factor group, characterization in terms of kernels of homomorphisms. Alternating groups as commutator subgroups.
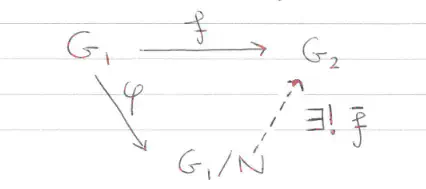
7. Homomorphism and Isomorphism Theorems: with as corrolary the characterization of normal subgroups of factor groups.
8. Group Actions: stabilisers, orbits, groups of prime order. Centralizer. Transitive actions.
9. Automorphisms: the automorphism group, inner automorphisms, characteristic subgroups. The semi-direct product.