Game Theory
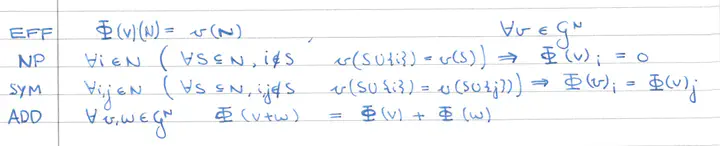 The four defining axioms of the Shapley value.
The four defining axioms of the Shapley value.Chapters
Chapter 1-4: Cooperative Game Theory.
- TU games, distributions, imputations, additive games, simple games, monotonous simple games, core, characterization using veto-players and dictators.
- Shapley value (a distribution), TU games as a linear space. Axiomatic characterization of Shapley value in terms of Additivity, Null-player property, Symmetry and Efficiency.
- Proof of uniqueness of the Shapley value for this characterization using unanimity games as a basis for the space of TU games. Convex TU games, characterization of their core as the convex hull of marginal vectors. Shapley value for monotonous simple games in terms of swings; motivation and definition of the normalized Banzhaf-Coleman index.
- Bankrupcy games, distribution rules. Nucleolus and unicity of its single element (proof omitted). The nucleolus underpins a distribution rule found already in the Talmud.
Chapter 5-6: Non-Cooperative Game Theory.
- (Zero sum) matrix games, mixed strategies. Maximin and minimax strategies. Matrix lemma of alternatives and from this the Minimax Theorem.
- Bimatrix games, best responses, Nash equilibria.